Craig, B: Introduction to the Practice of Statistics
In dit document staat alle belangrijke informatie voor het tentamen van onderzoekspracticum 2.
Wil jij geen samenvatting van 90 pagina's, maar een kortere samenvatting waar wel alle belangrijke punten in staan? Dan is deze samenvatting goed voor jou!
Extensive summary Craig, B: Introduction to the Practice of Statistics - Statistics
Summary Lectures and Readings: Statistics 1 - Introduction (FSWPE1-032)
Detailed Summary: Lectures and Readings STATISTICS 2.2 FSWPE2-022
All for this textbook (11)
Written for
Universiteit Leiden (UL)
Pedagogische Wetenschappen
Onderzoekspracticum 2 (6471OP2)
All documents for this subject (35)
Seller
Follow
vanpeltvera
Reviews received
Content preview
ONDERZOEKSPRACTCUM 2
steekproef populatie
gemiddelde 𝑥̅ 𝜇
Spreiding / standaarddeviatie s 𝜎
Standaardformules
𝑥𝑖
• 𝜇 = ∑𝑁 𝑖=1 𝑁 → gemiddelde in populatie
(𝑥𝑖− 𝑥̅ )2
• 𝜎 = √ ∑𝑁
𝑖=1 𝑁
→ standaarddeviatie in populatie
1
• 𝑥̅ = 𝑛
∑ 𝑥𝑖 → steekproefgemiddelde
1
• 𝑠= √ ∑(𝑥𝑖− 𝑥̅ )2 → standaarddeviatie van de steekproef
𝑛−1
• 𝜎2 → variantie in de populatie
• 𝑠2 → variantie in de steekproef
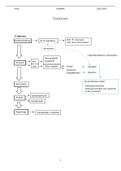
Toetsingsschema
• goede onderzoeksvraag
• situatieschets tekenen
• hypothesen opstellen (h0 en Ha) → 1 of 2 zijdig
• toets kiezen
• significantieniveau kiezen
• toetsstatistiek berekenen (t- waarde nu)
• zoek in tabel wat de bijbehorende p-waarde is
• beslissing: p<a → Ha, p>a → H0
• inhoudelijke conclusie geven (in normaal Nederlands of Engels)
ONE SAMPLE T-TOETS
Steekproevenverdeling = verdeling van de gemiddelden van alle mogelijke steekproeven met grootte n.
• Gemiddelde van steekproevenverdeling = gemiddelde van populatie = μ
• Normaalverdeling
• Steekproevenverdeling standaardiseren → van elke steekproef een Z-waarde berekenen
𝑥̅ −𝜇
➔ 𝑧 = 𝜎⁄ 𝑛0
√
• De σ is vrijwel nooit bekend, maar wordt vaak geschat op basis v.d. steekproef. Er kan geen Z
uitgerekend worden, dus gebruiken we t (student verdeeld)
𝑥̅ −𝜇
➔ 𝑡 = 𝑠⁄ 𝑛0 (met df = n – 1) → one sample t-test
√
BETROUWBAARHEIDSINTERVAL
• Beste schatting van μ op basis van de steekproef
𝑠
➔ 𝐶𝐼 = 𝑥̅ ± 𝑡 ∗ 𝑛 (met df = n -1) → beste schatting van μ +/- de foutenmarge
√
• μ valt met C% zekerheid binnen het interval
• hoe groter t, hoe groter kans dat μ binnen interval ligt.
𝑠
• Standaard error : 𝑆𝐸 =
√𝑛
HYPOTHESETOETSEN
• H0: μ = waarde
• Ha: μ ≠ waarde
• Hoe groot is de kans dat de steekproef gevonden is als H0 waar is? Hoe kleiner de kans, hoe meer
bewijs tegen H0.
• Met de t-waarde kun je p-waarde opzoeken in tabel D (df = n-1). P-waarde = overschrijdingskans (de
kans dat de t behaald of overschreden wordt in de steekproef als H0 waar is.)
➔ Bij 2-zijdig toetsen doe je p x 2
➔ Is p < α (vaak .05) dan is de steekproef te bijzonder om H0 te geloven → H0 verwerpen, Ha
accepteren
, ONE-WAY DESIGN
Het is een oneway design als er één onafhankelijke variabele is
Gouden regels experiment:
- manipuleer tenminste 1 variabele
- zorg voor vergelijkbare groepen
- houd andere variabelen strikt gelijk
experimentele basisdesigns
- randomized groups
•
- Matched subjects
• Proefpersonen eerst ingedeeld in groepjes volgens een subject variabele (bijv IQ), de individuen in
een groepje worden vervolgens random verdeeld over de condities
- Repeated measures
•
• Verschillende condities, met dezelfde proefpersonen
• = 2weg design (want 2 onafhankelijke variabele worden gemanipuleerd)
• Counterbalancing / cross-over → volgorde condities word ook gemanipuleerd
DE GEPAARDE T-TOETS
Op grond van een steekproef aannemelijk maken dat er een verschil is tussen twee populatiegemiddelden, dmv:
• Verschil tussen voor en nameting
• Verschil in populatiegemiddelden tussen twee verschillende Synoniemen:
groepen gepaarde t-toets (paired t-test)
afhankelijke t-toets (dependent t-test)
Verschilscores within subjects t-test
• Gaat om verschil tussen twee metingen bij dezelfde of gematchte MMC: matched pairs t procedures
proefpersonen SPSS: paired-samples T Test
• Verschil in gemiddelden = gemiddelde van de verschillen
• d= difference
➔ x1 – x2
𝑥̅ −𝜇
• 𝑡 = ⁄ 0 (met df = n-1) → 𝑥̅ gaat over het gemiddelde van de verschilscores. μ vaak als 0
𝑠𝑑 √𝑛
• p-waarde opzoeken in tabel D
➔ je toetst 2-zijdig, dus p * 2
• p<a → Ha, p>a → H0
Hypothesen
• H0: μd = 0 (μochtend = μavond)
• Ha: μd ≠ 0 (μochtend ≠ μavond)
Betrouwbaarheidsinterval
𝑠
• 𝐶𝐼 = 𝑥̅ ± 𝑡 ∗ → 𝑥̅ gaat over het gemiddelde van de verschilscores
√𝑛
➔ Foutenmarge = standaardfout verschilscores * de kritieke t (te vinden in tabel D (df= n-1)
DE INDEPENDENT SAMPLES T-TEST
• Metingen afkomstig van verschillende proefpersonen die niks met elkaar te maken hebben? →
independent t-test
The benefits of buying summaries with Stuvia:
Guaranteed quality through customer reviews
Stuvia customers have reviewed more than 700,000 summaries. This how you know that you are buying the best documents.
Quick and easy check-out
You can quickly pay through credit card or Stuvia-credit for the summaries. There is no membership needed.
Focus on what matters
Your fellow students write the study notes themselves, which is why the documents are always reliable and up-to-date. This ensures you quickly get to the core!
Frequently asked questions
What do I get when I buy this document?
You get a PDF, available immediately after your purchase. The purchased document is accessible anytime, anywhere and indefinitely through your profile.
Satisfaction guarantee: how does it work?
Our satisfaction guarantee ensures that you always find a study document that suits you well. You fill out a form, and our customer service team takes care of the rest.
Who am I buying these notes from?
Stuvia is a marketplace, so you are not buying this document from us, but from seller vanpeltvera. Stuvia facilitates payment to the seller.
Will I be stuck with a subscription?
No, you only buy these notes for $5.39. You're not tied to anything after your purchase.
