Tentamen (uitwerkingen)
Core Pure Mathematics
- Vak
- Instelling
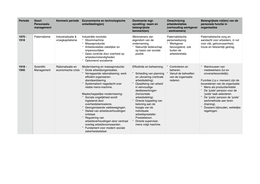
Given that z1 = 3cos π3 + isin π3 z = 2cos12π − isin12π (a) write down the exact value of (i) | z1z2 | (ii) arg (z1z2) (2) Given that w = z1z2 and that arg (wn) = ...
[Meer zien]