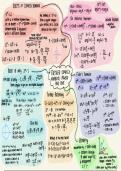
Summary AQA A Level Further Maths Year 2 Pure Topics Notes
4 views 0 purchase
Course
All Pure Year 2 Further Maths AQA A Level Topics
Institution
AQA
Second year pure notes of a past AQA A Level Further Maths student, were incredibly useful to facilitate getting an A* in AQA Further Maths in 2024. Includes all second year pure topics of AQA further maths, cohesive and includes both notes and example questions. Studying mathematics at university ...
Zu W =
the solutions of zn = w
write modulus argument form
w in form De moivre's theorem :
includes fractions
a regular polygon
Use de moivres e zn un(cosno + isinno negative
with vertices on circle
isino)"
=
a
zn =
(r(coso + = r(cosno + isinno) powers
compare moduli & arguments centred at the origin
Write n different solutions :
stil
THINK ABOUT (4i) =
4
ARGAND FOR START VALUE
- arg( +
i) = arg(i) =
/
z 45 4i arg(45 + 4i) F
=
= +
Iti(cos + isin)
,
=
r (10530 + isin30) +
/6 ,
-
2π 30 =
(l i) 32(05 isin)
+ = +
828
*
145 + 4il = =
2
= 32(205 /2
+
+ isin/2)
= 32 ;
Roots of mity ze
Euler's formula :
nth roots of unity - 1 ,
ee ... cio-COSO + isino
reio-r(coso + isino
form a
regular n-gon on an argand diagram reio z= reio
ei - z
2
=
=
nth
root
S
=
Wi =
(e)" =
Wi = 0 1 2 ,3
. .
... n -
1
further factorising Z-zez we zei e2 + 3i = 22g
It Wi 0
each ROU is (2 +... + Wn e ((053 + isin3)
+ =
(2) (e)
a "
(z W((z-W*) [Re(W) + IWR
=
power of W
,
-
= z zws
wa
-
-
... + Wh
=
It Wit Wat ...
= I + 2 + + Z
= - 7 32
.
+ 1 . 04i
= 2e
Z" -81 z in Cartesian
= -w =
+ 3i
(e(n3)2
-
Sle iπr4 8)r 3
+3i
1- w
rugino 8) = =
32
e
= -
= =
W 4
: ezn3 el3insli
=
48 = , 3 5
0 =
:
Fifth ROU
, ,
4(c0s[ + isin)
isin (In 27)
* :
WY = W
9((0S(In27) +
13 3 i
=
* =
z +
wi (w2) =
e e, e
=
=
-8 89-1 38i
I 25 - 21
. .
Re(w") Re(w) = ,
, =
=
Re(w3) Re(w) =
product of two real factors
isinos
COS (z zi)(z zu) z2 352z + 9
Geometry
cosRe(W) = -
-
=
Re(W)
-
Sin50 + 5 sin40 + 10 sin30 + 10sin20 + 5 sinO
= 32(OS9 Jin
The benefits of buying summaries with Stuvia:
Guaranteed quality through customer reviews
Stuvia customers have reviewed more than 700,000 summaries. This how you know that you are buying the best documents.
Quick and easy check-out
You can quickly pay through credit card or Stuvia-credit for the summaries. There is no membership needed.
Focus on what matters
Your fellow students write the study notes themselves, which is why the documents are always reliable and up-to-date. This ensures you quickly get to the core!
Frequently asked questions
What do I get when I buy this document?
You get a PDF, available immediately after your purchase. The purchased document is accessible anytime, anywhere and indefinitely through your profile.
Satisfaction guarantee: how does it work?
Our satisfaction guarantee ensures that you always find a study document that suits you well. You fill out a form, and our customer service team takes care of the rest.
Who am I buying these notes from?
Stuvia is a marketplace, so you are not buying this document from us, but from seller msevabowen. Stuvia facilitates payment to the seller.
Will I be stuck with a subscription?
No, you only buy these notes for $13.55. You're not tied to anything after your purchase.
