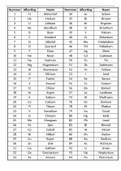
Verschillende t-toetsen;
1) T-test voor 1 steekproef en 1 variabele, bij deze t-toets ben je geïnteresseerd in het
populatie gemiddelde
2) T- test voor 2 onafhankelijke steekproeven waaraan je 1 variabele meet, je bent
geïnteresseerd in het verschil in populatie gemiddelde tussen de twee steekproeven.
3) Paired T-test, bij deze toets heb je 1 steekproef waaraan je twee variabelen meet. Je
kijkt of de verschil normaal verdeeld is!
Voorbeeld; Je meet de score van studenten voor een training = x en de score van
diezelfde studenten na de training = y.
Je bent geïnteresseerd in het gemiddelde verschil µd = x – y .
4) T-test voor lineaire regressie model, hier ben je geïnteresseerd in de lineaire relatie
tussen een variabele x en de variabele y. De observaties/metingen y1, y2, y3 enz. zijn
normaal verdeelt met µy= B0 + B1X
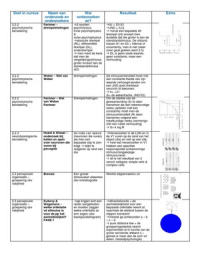
Overzicht van de symbolen;
Ῡ= steekproef gemiddelde
µ = verwachte waarde ( populatie gemiddelde)
σῩ = populatie standaardafwijking enkele trekking / wortel n
σ = populatiestandaardafwijking
s = steekproef standaardafwijking
σy = populatie standaardafwijking enkele trekking
µ0 = de verwachte gemiddelde van de nulhypothese
α = significantie niveau
df = aantal vrijheidsgraden = n – 1 of n – 2
n = grootte van de steekproef
sd= standaardafwijking steekproef
se(mean) = standard error mean ofwel sd / √n
σ2 = variantie
een dakje staat altijd voor een schatting.
, Tutorial 1 + 2
Met een Q,Q plot valt te controleren of een waarde normaal verdeelt is. De punten in de
grafiek zullen dan langs de lijn in de grafiek moeten liggen.
𝜎𝑦
De populatie standaardafwijking van het gemiddelde σῩ = (populatie
√𝑛
standaardafwijking enkele trekking gedeeld door de wortel n)
Stel je neemt een steekproef uit een populatie. Deze populatie heeft een verwachte waarde
(ofwel een populatie gemiddelde = µ). Als een voorbeeld, de populatie gemiddelde van een
populatie van 10000 mensen heeft een verwachte waarde van 50 kg lichaamsgewicht.
Een steekproef gemiddelde is een schatting op een bepaald punt voor deze verwachte
waarde op dat bepaalde punt. Om een uitspraak te doen over de nauwkeurigheid van deze
puntschatting, gebruik je een betrouwbaarheidsinterval.
Een betrouwbaarheidsinterval heeft de vorm van een schatting + en – een bepaalde
foutmarge. Deze foutmarge word bepaald door het betrouwbaarheid coëfficiënt.
Betrouwbaarheid coëfficiënt = (1 – α ) hierbij is α = het significantie niveau.
Stel je wilt een 95% betrouwbaarheidsinterval, dan zal de α 0,05 bedragen. Dit is de mate
van onzekerheid. Hier verwacht je dus 5 fouten op de 100, dus 5 van de 100 intervallen
zullen hier de verwachte waarde niet bevatten. Kort gezegd; In 95% van alle mogelijke
steekproeven zal het bijbehorende 95%-betrouwbaarheidsinterval de daadwerkelijke
populatie gemiddelde bevatten.
De kans dat de werkelijke verwachte waarde ofwel de populatie gemiddelde niet in het
berekende interval ligt is hier 5%. (Een andere steekproef zal een ander
betrouwbaarheidsinterval hebben)
Als de populatiestandaardafwijking bekend is gebruik je de Z-waarde. De Z-waarde verteld
ons hoeveel standaardafwijkingen een resultaat verschild met het gemiddelde µ. Een
𝜎
betrouwbaarheidsinterval word dan als volgt gevormd; Ῡ ± Z(α/2) ×
√𝑛
Is de σ niet bekend gebruik je de t-waarde. We kunnen de populatie standaardafwijking
schatten door middel van de s (steekproef standaardafwijking).
𝑠
Standaardafwijking gemiddelde SE(Ῡ) = √𝑛 waarbij s = standaardafwijking steekproef
Als de n groter is dan 30 gebruik je de Z-test, als de n kleiner is dan 30 gebruik je de t-test. Je
gebruikt bij een kleine steekproef de student - t verdeling. Deze verdeling heeft een
bepaalde aantal vrijheidsgraden (df). Door de kleinere steekproef met bijvoorbeeld slechts
een n = 2, zal de top van de normale verdeling wat zakken. Doordat de oppervlakte onder de
verdeling nog steeds gelijk aan 1 moet zijn, zullen de staarten van de verdeling wat omhoog
gaan. Hierdoor zal de t-score hoger worden dan de Z-score.