Garantie de satisfaction à 100% Disponible immédiatement après paiement En ligne et en PDF Tu n'es attaché à rien
logo-home
Recherché précédemment par vous
Recherché précédemment par vous
logo
Limites de fonction 3,49 €
Ajouter au panier
Accédez rapidement à
Aperçu
  2.  
  3. Lycée
  4.  
  5. Lycée
  6.  
  7. Mathématique

Notes de cours

Limites de fonction
 3 vues  0 fois vendu

Le chapitre sur les limites de fonction en analyse mathématique explore la notion de limite d'une fonction en un point ou à l'infini, un concept clé pour comprendre le comportement des fonctions lorsque les valeurs d’entrée s’approchent d’un certain point. Ce chapitre aborde les définiti...

[Montrer plus]

Aperçu 2 sur 11  pages

Infos sur le Document

  • 15 novembre 2024
  • 11
  • 2024/2025
  • Notes de cours
  • Chiousse thomas
  • Toutes les classes

Sujets

École, étude et sujet

  • Lycée
  • Lycée
  • Mathématique
  • 1
Tous les documents sur ce sujet (113)

Vendeur

avatar-seller
thomaschiousse2007

Aperçu du contenu

Chapitre 3
Limites de fonction

3.1 Limite in
nie en l'in
ni
3.1.1 Dé
nition
Dé
nition 1
Soit f une fonction dé
nie sur un intervalle de la forme ]α, +∞[ ou [α, +∞[.
1. On dit que f tend vers +∞ quand x tend vers +∞ si et seulement si tout inter-
valle de la forme ]A, +∞[ contient f (x) pour x positif assez grand. On écrit alors
lim f (x) = +∞.
x→+∞
2. On dit que f tend vers −∞ quand x tend vers +∞ si et seulement si tout inter-
valle de la forme ]−∞, A[ contient f (x) pour x positif assez grand. On écrit alors
lim f (x) = −∞.
x→+∞




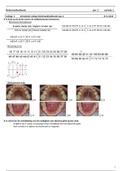
Pour tout réel A, f (x) > A dès que x est Pour tout réel A, f (x) < A dès que x est
su
samment grand lim f (x) = +∞ su
samment grand lim f (x) = −∞
x→+∞ x→+∞




Dé
nition 2
Soit f une fonction dé
nie sur un intervalle de la forme ]−∞, α[ ou ]−∞, α].
1. On dit que f tend vers +∞ quand x tend vers −∞ si et seulement si tout intervalle
de la forme ]A, +∞[ contient f (x) pour x négatif assez grand en valeur absolue. On
écrit alors lim f (x) = +∞.
x→−∞
2. On dit que f tend vers −∞ quand x tend vers −∞ si et seulement si tout intervalle
de la forme ]−∞, A[ contient f (x) pour x négatif assez grand en valeur absolue. On
écrit alors lim f (x) = −∞.
x→−∞




24

, Pour tout réel A, f (x) > A dès que x est négatif Pour tout réel A, f (x) < A dès que x est négatif
et su
samment grand en valeur absolue et su
samment grand en valeur absolue
lim f (x) = +∞ lim f (x) = −∞
x→−∞ x→−∞



3.1.2 Limites de référence in
nies en l'in
ni
Théorème 3

1. a. Pour tout entier naturel non nul n, x→+∞
lim xn = +∞
b. Pour tout entier naturel non nul p, lim x2p = +∞ et lim x2p+1 = −∞ ou
x→−∞ x→−∞
encore, pour tout entier naturel non nul n,

+∞ si n est pair
®
lim xn =
x→−∞ −∞ si n est impair
√
2. lim
x→+∞
x = +∞



√
Démonstration. Nous allons démontrer que lim x = +∞ et que lim x2 = +∞
x→+∞ √ x→−∞
• Soit A un réel. Si A < 0, alors pour √tout réel
√ x ⩾ 0, x > A. √
Si A ⩾ 0, alors pour x √ ⩾ A2 , on a x > A2 (par stricte croissance de la fonction t 7→ t
sur [0, +∞[) ou encore x > A. √
Ainsi, tout intervalle de la forme ]A, +∞[ contient x pourvu que x soit su
samment grand
et donc √
lim x = +∞
x→+∞

• Soit A un réel. Si A < 0, alors pour tout
√ réel x, x2 > A. √ 2
2

Si A ⩾ 0, alors pour tout réel x ⩽ − A, on a x > (− A) (par stricte décroissance de la
fonction t 7→ t2 sur ]−∞, 0]) ou encore x2 > A.
Ainsi, tout intervalle de la forme ]A, +∞[ contient x2 pourvu que x soit négatif et su
samment
grand en valeur absolue. Donc
lim x2 = +∞
x→−∞

■




25

Les avantages d'acheter des résumés chez Stuvia:

Qualité garantie par les avis des clients

Qualité garantie par les avis des clients

Les clients de Stuvia ont évalués plus de 700 000 résumés. C'est comme ça que vous savez que vous achetez les meilleurs documents.

L’achat facile et rapide

L’achat facile et rapide

Vous pouvez payer rapidement avec iDeal, carte de crédit ou Stuvia-crédit pour les résumés. Il n'y a pas d'adhésion nécessaire.

Focus sur l’essentiel

Focus sur l’essentiel

Vos camarades écrivent eux-mêmes les notes d’étude, c’est pourquoi les documents sont toujours fiables et à jour. Cela garantit que vous arrivez rapidement au coeur du matériel.

Foire aux questions

Qu'est-ce que j'obtiens en achetant ce document ?

Vous obtenez un PDF, disponible immédiatement après votre achat. Le document acheté est accessible à tout moment, n'importe où et indéfiniment via votre profil.

Garantie de remboursement : comment ça marche ?

Notre garantie de satisfaction garantit que vous trouverez toujours un document d'étude qui vous convient. Vous remplissez un formulaire et notre équipe du service client s'occupe du reste.

Auprès de qui est-ce que j'achète ce résumé ?

Stuvia est une place de marché. Alors, vous n'achetez donc pas ce document chez nous, mais auprès du vendeur thomaschiousse2007. Stuvia facilite les paiements au vendeur.

Est-ce que j'aurai un abonnement?

Non, vous n'achetez ce résumé que pour 3,49 €. Vous n'êtes lié à rien après votre achat.

Peut-on faire confiance à Stuvia ?

4.6 étoiles sur Google & Trustpilot (+1000 avis)

52928 résumés ont été vendus ces 30 derniers jours

Fondée en 2010, la référence pour acheter des résumés depuis déjà 14 ans

Commencez à vendre!
3,49 €
  • (0)
Ajouter au panier
Ajouté