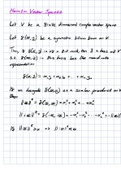Linear Algebra 2 (MAA241)
Loughborough University (LU)
All 8 results
Sort by
Notes defining Hermitian forms on vector spaces, including various theorems that can be used when working with or finding them.
Notes defining Bilinear Forms, Matrices of Bilinear Forms and Coordinate Representations. Covers concepts such as Rank, Symmetric and Skew-Symmetric Matrices, and Congruence.
Notes defining Euclidean Vector Spaces, Gram Matrices and Orthogonal Matrices; with examples of each. Also includes a proof of the Cauchy-Bunyakovsky-Schwarz Inequality.

-
Linear Algebra 2 - Quadratic Forms on Euclidean Spaces: Algorithm of Finding a Canonical Basis
- Lecture notes • 22 pages • 2022
-
- £2.99
- + learn more
These notes go into more explicit detail on the practical algorithms for converting a quadratic form into canonical form. They also include a number of examples to help grasp it.
Notes on solving Cauchy problems using matrix concepts such as matrix powers, diagonalisability and eigenspaces. Includes various examples including the Fibonacci sequence.
We have previously defined both Quadratic and Bilinear Forms. This set of notes covers the process for converting these to Canonical Form.
Notes defining and covering theorems related to Orthogonal Matrices.
Notes discussing theorems for quadratic forms on ℝ vector spaces including rigorous proofs.

How much did you already spend on Stuvia? Imagine there are plenty more of you out there paying for study notes, but this time YOU are the seller. Ka-ching! Discover all about earning on Stuvia