2 3)
. .
Analysis Design ,
and Comparison of Algorithms
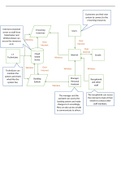
Analysis of algorithms
Time
complexity :
↳ how much time it requires to solve a particular problem
↳
big (shows the effectiveness of
measured
using O notation an
algorithm
↳
upper limit for the amount of time taken relative to the number
it of data elements
shows an
given
as an input
↳
allows
you
to predict the amount of time it takes for an
algorithm to finish guien the
number of data elements
Big O notation Name Description
O(1) Constant time the amount of time taken to complete an
complexity algorithm is independent from the number of
elements inputted
O(n) Linear
Lime the amount of time taken to complete an
complexity algorithm is directly proportional to the number
of elements inputted
O(nz) Polynomial/quadratic the amount of time taken to complete an
time the
complexity algorithm is
directionally proportional to
elements
square of the inputted
O(nt) the amount of time taken to complete
Polynomial time an
to the elements
complexity algorithm is
directly proportional
Inputted to the
power of n
O(24) Exponential time the amount of time taken to complete an
complexity algorithm will double with additional item
every
Ollogn) Logarithmic time the time taken to complete an
algorithm will
complexity increase at a smaller rate as the number of
elements inputted
:
graphs
0(24) O(n))
I
worst O(22) O(n')
Onlog(n)
O(n)
O(n)
-
O(log(n)
best ~O(1)
n
Ollogn)
O(1)
Input Size <
, Space complexity :
↳ amount
of storage the algorithm takes
↳
Commonly expressed using Big O notation
algorithms store extra data when they make
↳ a isn't ideal
copy ,
it is not idea to make copies
↳ When
working with lots of data ,
a
good
↳ this
lakes up lots of
storage which is expensive
Designing Algorithms:
series of steps to complete
↳
algorithm > a task a
-
designing the main objective is to complete thelask then to the best time
↳ When
, , get
and space
complexity
↳ to reduce
space complexity you ,
make sure
you perform
all of the changes on the
original
data
pieces of
to reduce time and the number of items
↳
complexity try ,
to reduce the embedded loops ,
have to complete the operations on
you
Comparison of Algorithms
Best and worst case scenarios :
,
average
Searching
Time complexity Sorting Time
complexity Space :
Best Worst Algorithm
algorithms Average Bes↓ Average Worst
linear search O(1) O(n) O(n) bubble O(n) Oln't On' I
binarysarray O(1) Ollogn) Ollogn) insertion O(n) O(n' O(nz) I
binarystree O(1) Ollogn) O(n) merge Onlogn) OCnlogn) OCnlogn) n
hashing O(1) 0(1) O(n)
quick OCnlogn) OCnlogn) O(n') logn
breadth/depth-0(1) ON E) +
O(v2)
vertices +
first of graph edges
Comparing linear and binary
linear search
binary search
Data set items don't have to be stored in order Items must be ordered to work
Start location start at first item start at middle item
searching search each item in sequence until halve the set of items to search
the item is found or there are no
after each comparison until the
more items to check item is found or there are no more
items to check
implementation Canbe implemented using an Can be implemented using an
array
or linked list array or binary tree
items New items added at the end - New items must be added in the
adding are
quick correct place to maintain the
number ofitems -
can be slow
suitability Suitable for a small number Suitable for
&
a
large number of
of items utems
. .
Analysis Design ,
and Comparison of Algorithms
Analysis of algorithms
Time
complexity :
↳ how much time it requires to solve a particular problem
↳
big (shows the effectiveness of
measured
using O notation an
algorithm
↳
upper limit for the amount of time taken relative to the number
it of data elements
shows an
given
as an input
↳
allows
you
to predict the amount of time it takes for an
algorithm to finish guien the
number of data elements
Big O notation Name Description
O(1) Constant time the amount of time taken to complete an
complexity algorithm is independent from the number of
elements inputted
O(n) Linear
Lime the amount of time taken to complete an
complexity algorithm is directly proportional to the number
of elements inputted
O(nz) Polynomial/quadratic the amount of time taken to complete an
time the
complexity algorithm is
directionally proportional to
elements
square of the inputted
O(nt) the amount of time taken to complete
Polynomial time an
to the elements
complexity algorithm is
directly proportional
Inputted to the
power of n
O(24) Exponential time the amount of time taken to complete an
complexity algorithm will double with additional item
every
Ollogn) Logarithmic time the time taken to complete an
algorithm will
complexity increase at a smaller rate as the number of
elements inputted
:
graphs
0(24) O(n))
I
worst O(22) O(n')
Onlog(n)
O(n)
O(n)
-
O(log(n)
best ~O(1)
n
Ollogn)
O(1)
Input Size <
, Space complexity :
↳ amount
of storage the algorithm takes
↳
Commonly expressed using Big O notation
algorithms store extra data when they make
↳ a isn't ideal
copy ,
it is not idea to make copies
↳ When
working with lots of data ,
a
good
↳ this
lakes up lots of
storage which is expensive
Designing Algorithms:
series of steps to complete
↳
algorithm > a task a
-
designing the main objective is to complete thelask then to the best time
↳ When
, , get
and space
complexity
↳ to reduce
space complexity you ,
make sure
you perform
all of the changes on the
original
data
pieces of
to reduce time and the number of items
↳
complexity try ,
to reduce the embedded loops ,
have to complete the operations on
you
Comparison of Algorithms
Best and worst case scenarios :
,
average
Searching
Time complexity Sorting Time
complexity Space :
Best Worst Algorithm
algorithms Average Bes↓ Average Worst
linear search O(1) O(n) O(n) bubble O(n) Oln't On' I
binarysarray O(1) Ollogn) Ollogn) insertion O(n) O(n' O(nz) I
binarystree O(1) Ollogn) O(n) merge Onlogn) OCnlogn) OCnlogn) n
hashing O(1) 0(1) O(n)
quick OCnlogn) OCnlogn) O(n') logn
breadth/depth-0(1) ON E) +
O(v2)
vertices +
first of graph edges
Comparing linear and binary
linear search
binary search
Data set items don't have to be stored in order Items must be ordered to work
Start location start at first item start at middle item
searching search each item in sequence until halve the set of items to search
the item is found or there are no
after each comparison until the
more items to check item is found or there are no more
items to check
implementation Canbe implemented using an Can be implemented using an
array
or linked list array or binary tree
items New items added at the end - New items must be added in the
adding are
quick correct place to maintain the
number ofitems -
can be slow
suitability Suitable for a small number Suitable for
&
a
large number of
of items utems