LANGUAGE AND COMPUTATION – SUMMARY
Topics:
• Formal language theory and linguistics
• Finite State Automata + Regular Expressions
• Subregular languages
• Probabilistic grammars
• Pushdown Automata + CFGs
WEEK 1: INTRODUCTION
In the linguistics programme, we view language and cognition both from an empirical
viewpoint and from the perspective of formal modelling. For both aspects we use
instruments from mathematics, logic and computer science.
Topics
• Formal foundations of regular languages (week 2 + week 3 lecture)
• Quantitative approaches & linguistic theory (week 3 lab + week 4)
• Formal foundations of context-free languages (week 5 + week 6 lecture)
• Finding structure in language (week 6 lab + week 7)
Formal Foundations
Language is related to both variation and invariance. The use of language is a cognitive
ability characteristic for humans and there are over 7000 languages worldwide. The
challenge is to discover any universals or tendencies among this diversity. These universals
might lie in the realm of computational complexity and to assess this we need to do some
formal modelling. To do this, we use instruments from mathematics, logic and computer
science: grammars as algorithms, grammars as logical systems and recursion.
The concept of language on different levels
➢ the language of mathematics: sets, relations, functions
➢ the language of logic: patterns of valid reasoning
➢ programming languages: “recipes” for computation
,➢ natural language: English, Yoruba, Quechua, Vietnamese … (which we seek to model)
Patterns, grammar and automata
There are some questions such as distinguishing between meaningful patterns and noise,
how patterns in languages differ in complexity and how to measure this and how our
processing system can handle these patterns that can be viewed from two complementary
perspectives. Furthermore, this approach is not limited to natural language.
- formal grammars: “recipes” to generate patterns
- automata: the models of (step-by-step) computation that correspond to these.
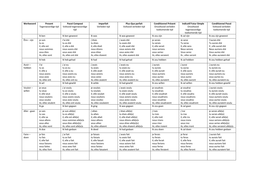
The table above describes families of languages (grammars/automata) with increasing
expressivity. There is a trade-off however: expressivity is directly proportional to complexity.
The goal or desire would be to have a proper balance between expressivity and comfortable
computational complexity.
There are 4 levels – Type-3, Type-2, Type-1, Type-0. With every level, the grammar becomes
less restrictive in rules and more powerful but more complicated to automate. Every level is
also a subset of the subsequent level.
Type-3: Regular Grammar - most restrictive of the set, they generate regular languages.
They must have a single non-terminal on the left-hand-side and a right-hand-side consisting
of a single terminal or single terminal followed by a single non-terminal.
Type-2: Context-Free Grammar - generate context-free languages, a category of immense
interest to NLP practitioners. Here all rules take the form A → β, where A is a single non-
terminal symbol and β is a string of symbols. Natural languages fall in this category.
Type-1: Context-Sensitive Grammar - the highest programmable level, they generate
context-sensitive languages. They have rules of the form α A β → α γ β with A as a non-
terminal and α, β, γ as strings of terminals and non-terminals. Strings α, β may be empty,
but γ must be nonempty. Dutch and Swiss German containing grammatical constructions
with cross-serial dependencies.
,Type-0: Recursively enumerable grammar - are too generic and unrestricted to describe the
syntax of either programming or natural languages.
TYPE 3: REGULAR PATTERNS AND FINITE STATE AUTOMATA
The structure of syllables can be described as:
➢ start (onset): consonants (str is OK, but rts is not)
➢ core (nucleus): vowels (oi is OK, but io is not)
➢ tail (coda): consonant (rts is OK, but str is not)
The patterns above are regular patterns, and the processing is finite state automaton.
- grammar: regular expressions, atomic (simple symbols) or complex.
- operations: concatenation (one after the other), choice and repetition.
- neutral elements: 1 for empty string and 0 for empty language.
, TYPE 2: CONTEXT FREE AND PUSH-DOWN AUTOMATA
For mirror image words such as “bib”, “deed”, “kayak” and “rotator” and also sentences
such as “Live on, Time; emit no evil”, the computational power of finite state automata is
insufficient. The processing model of type 2 grammars is like a finite state automaton, but it
also has a memory of “FIRST IN, LAST OUT” (FILO) type.
- recognizing a palindrome with a pushdown automaton: transitions in the automaton
depend on the current input symbol and the most recent symbol added to the memory/
- recursion is also observed: the “recipe” for palindromes refers to itself: a mirror image
word starts and ends with two copies of the same letter with another mirror image word
sandwiched in between. Tree structure below.
X + mirror word + X -> amo + k + oma
Topics:
• Formal language theory and linguistics
• Finite State Automata + Regular Expressions
• Subregular languages
• Probabilistic grammars
• Pushdown Automata + CFGs
WEEK 1: INTRODUCTION
In the linguistics programme, we view language and cognition both from an empirical
viewpoint and from the perspective of formal modelling. For both aspects we use
instruments from mathematics, logic and computer science.
Topics
• Formal foundations of regular languages (week 2 + week 3 lecture)
• Quantitative approaches & linguistic theory (week 3 lab + week 4)
• Formal foundations of context-free languages (week 5 + week 6 lecture)
• Finding structure in language (week 6 lab + week 7)
Formal Foundations
Language is related to both variation and invariance. The use of language is a cognitive
ability characteristic for humans and there are over 7000 languages worldwide. The
challenge is to discover any universals or tendencies among this diversity. These universals
might lie in the realm of computational complexity and to assess this we need to do some
formal modelling. To do this, we use instruments from mathematics, logic and computer
science: grammars as algorithms, grammars as logical systems and recursion.
The concept of language on different levels
➢ the language of mathematics: sets, relations, functions
➢ the language of logic: patterns of valid reasoning
➢ programming languages: “recipes” for computation
,➢ natural language: English, Yoruba, Quechua, Vietnamese … (which we seek to model)
Patterns, grammar and automata
There are some questions such as distinguishing between meaningful patterns and noise,
how patterns in languages differ in complexity and how to measure this and how our
processing system can handle these patterns that can be viewed from two complementary
perspectives. Furthermore, this approach is not limited to natural language.
- formal grammars: “recipes” to generate patterns
- automata: the models of (step-by-step) computation that correspond to these.
The table above describes families of languages (grammars/automata) with increasing
expressivity. There is a trade-off however: expressivity is directly proportional to complexity.
The goal or desire would be to have a proper balance between expressivity and comfortable
computational complexity.
There are 4 levels – Type-3, Type-2, Type-1, Type-0. With every level, the grammar becomes
less restrictive in rules and more powerful but more complicated to automate. Every level is
also a subset of the subsequent level.
Type-3: Regular Grammar - most restrictive of the set, they generate regular languages.
They must have a single non-terminal on the left-hand-side and a right-hand-side consisting
of a single terminal or single terminal followed by a single non-terminal.
Type-2: Context-Free Grammar - generate context-free languages, a category of immense
interest to NLP practitioners. Here all rules take the form A → β, where A is a single non-
terminal symbol and β is a string of symbols. Natural languages fall in this category.
Type-1: Context-Sensitive Grammar - the highest programmable level, they generate
context-sensitive languages. They have rules of the form α A β → α γ β with A as a non-
terminal and α, β, γ as strings of terminals and non-terminals. Strings α, β may be empty,
but γ must be nonempty. Dutch and Swiss German containing grammatical constructions
with cross-serial dependencies.
,Type-0: Recursively enumerable grammar - are too generic and unrestricted to describe the
syntax of either programming or natural languages.
TYPE 3: REGULAR PATTERNS AND FINITE STATE AUTOMATA
The structure of syllables can be described as:
➢ start (onset): consonants (str is OK, but rts is not)
➢ core (nucleus): vowels (oi is OK, but io is not)
➢ tail (coda): consonant (rts is OK, but str is not)
The patterns above are regular patterns, and the processing is finite state automaton.
- grammar: regular expressions, atomic (simple symbols) or complex.
- operations: concatenation (one after the other), choice and repetition.
- neutral elements: 1 for empty string and 0 for empty language.
, TYPE 2: CONTEXT FREE AND PUSH-DOWN AUTOMATA
For mirror image words such as “bib”, “deed”, “kayak” and “rotator” and also sentences
such as “Live on, Time; emit no evil”, the computational power of finite state automata is
insufficient. The processing model of type 2 grammars is like a finite state automaton, but it
also has a memory of “FIRST IN, LAST OUT” (FILO) type.
- recognizing a palindrome with a pushdown automaton: transitions in the automaton
depend on the current input symbol and the most recent symbol added to the memory/
- recursion is also observed: the “recipe” for palindromes refers to itself: a mirror image
word starts and ends with two copies of the same letter with another mirror image word
sandwiched in between. Tree structure below.
X + mirror word + X -> amo + k + oma