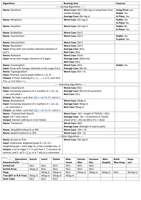
Dit is het grote overzicht met van de cursus Datastructures. Alle algorithms en datastructures staan erin in een mooi overzicht. Ook allerlei andere belangrijke dingen voor de course.
Algorithms Running time Features
----- Sorting Algorithms -----
Name: QuickSort Worst Case: Θ(n2) (Θ(n log n) using linear time Using Pivot: yes
median finding) Stable: Yes
Average Case: Θ(n log n) In Place: Yes
Name: MergeSort Worst Case: O(n log n) Stable: Yes
In Place: No
Name: HeapSort Worst Case: O(n log n) Stable: No
In Place: Yes
Name: BubbleSort Worst Case: O(n2)
Name: InsertionSort Worst Case: Θ(n2) Stable: Yes
In place: Yes
Name: SelectionSort Worst Case: O(n2)
Name: BucketSort Worst Case: O(n2)
Input: Array with real number elements between 0 Average Case: Θ(n)
and 1 Best Case: Θ(n)
Name: RadixSort Worst Case: O(nk)
Input: Array with integer elements of d digits Average Case: Θ(d(n+k))
Best Case: Θ(n)
Name: CountingSort Worst Case: Θ(n) Stable: Yes
Input: Array with interger elements in the range 0 to k Avarage Case: Θ(n+k)
Name: TopologicalSort Worst Case: Θ(V + E)
Input: Directed, acyclic graph (DAG) G = (V, E)
Output: A linear ordering of v1 ,v2 ,…, vn ∈ V, such that
if (vi ,vj ) ∈ E then i < j
----- Searching Algorithms -----
Name: LinearSearch Worst Case: Θ(n)
Input: Increasing sequence of n numbers A = ‹a1, a2, Average Case: Θ(n/2) (if successful)
…, an› and value v Best Case: Θ(1)
Output: An index i such that A[i] = v or NIL if v not in A
Name: BinarySearch Worst Case: Θ(log n)
Input: Increasing sequence of n numbers A = ‹a1, a2, Average Case: Θ(log n)
…, an› and value v Best Case: Θ(log n)
Output: an index i such that A[i] = v or NIL if v not in A
Name: Chained-Hash-Search Worst Case: O(1 + length of T[h(k)]) = O(n)
Input: List T and a key k Average Case: O(1 + # elements in T[h(k)]
Output: Element with key k in list T[h(k)] ahead of k) = Θ(1+α) (Θ(1) if m = Ω(n))
Name: TreeSearch Worst Case: Θ(h)
Average Case: Θ(length of search path)
Name: BreadthFirstSearch or BFS Worst Case: O(V + E)
Name: DepthFirstSearch or DFS Worst Case: Θ(V + E)
----- Other Algorithms -----
Name: Krustal or Prim Worst Case: O(E log V)
Input: undirected, weighted graph G = (V, E)
weighted graph = each edge (u, v) has a weight w(u, v)
Output: a set of edges T ⊂ E such that 1. T connects all
vertices, and 2. w(T) = ∑ (u, v) ∈ T w(u,v) is minimized
Voordelen van het kopen van samenvattingen bij Stuvia op een rij:
Verzekerd van kwaliteit door reviews
Stuvia-klanten hebben meer dan 700.000 samenvattingen beoordeeld. Zo weet je zeker dat je de beste documenten koopt!
Snel en makkelijk kopen
Je betaalt supersnel en eenmalig met iDeal, creditcard of Stuvia-tegoed voor de samenvatting. Zonder lidmaatschap.
Focus op de essentie
Samenvattingen worden geschreven voor en door anderen. Daarom zijn de samenvattingen altijd betrouwbaar en actueel. Zo kom je snel tot de kern!
Veelgestelde vragen
Wat krijg ik als ik dit document koop?
Je krijgt een PDF, die direct beschikbaar is na je aankoop. Het gekochte document is altijd, overal en oneindig toegankelijk via je profiel.
Tevredenheidsgarantie: hoe werkt dat?
Onze tevredenheidsgarantie zorgt ervoor dat je altijd een studiedocument vindt dat goed bij je past. Je vult een formulier in en onze klantenservice regelt de rest.
Van wie koop ik deze samenvatting?
Stuvia is een marktplaats, je koop dit document dus niet van ons, maar van verkoper royvandijk06. Stuvia faciliteert de betaling aan de verkoper.
Zit ik meteen vast aan een abonnement?
Nee, je koopt alleen deze samenvatting voor €4,48. Je zit daarna nergens aan vast.
