Samenvatting
Summary of Investment Management
Summary of the discussed chapters from the book "Investments)
[Meer zien]Voorbeeld 4 van de 59 pagina's
Voorbeeld 4 van de 59 pagina's
In winkelwagengesponsord bericht van onze partner
Gekoppeld boek
Titel boek:
Auteur(s):
- Uitgave:
- ISBN:
- Druk:
1 beoordeling
Door: siebe7 • 4 jaar geleden
Voorbeeld van de inhoud
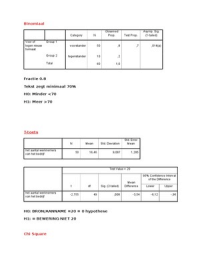
Chapter 5: Risk, Return, and the Historical Record5.1 Determinants of the Level of Interest Rates
The level of interest rates is perhaps the most important macroeconomic factor to consider in one’s investment
analysis. Forecasts of interest rates directly determine expected returns in the fixed-income market.
We have a good understanding of the fundamental factors that determine the level of interest rates:
1. The supply of funds from savers, primarily households.
2. The demand for funds from businesses to be used to finance investments in plant, equipment, and
inventories (real assets or capital formation).
3. The government’s net demand for funds as modified by actions of the Federal Reserve Bank.
4. The expected rate of inflation.
Real and Nominal Rates of Interest
An interest rate is a promised rate of return denominated in some unit of account over some time period.
What the real return is, depends upon what your money can buy today relative to what you could buy when
you deposited the money.
Nominal interest rate: the growth rate of your money
Real interest rate: the growth rate of your purchasing power
1+ r nom
(5.1) 1+r real =
1+i
A common approximation to this relation is:
(5.2) r real ≈ r nom −1
Rearranging (5.1):
r nom −i
(5.3) r real =
1+i
Conventional fixed income investments promise a nominal rate of interest. You can only infer the expected real
rate on these investments by adjusting the nominal rate for your expectation of the rate of inflation.
The Equilibrium Real Rate of Interest
Three basic factors determine the real interest rate:
Supply
Demand
Government actions
The nominal interest rate is the real rate plus the expected rate of inflation.
The supply curve slopes up from left to right because the higher real interest rate, the greater the supply of
household savings.
At higher real interest rates, households will choose to postpone some current consumption.
The demand curve slopes down from left to right because the lower the real interest rate, the more businesses
will want to invest in physical capital.
1
,The government and central bank can shift these supply and demand curves either to the right or to the left
through fiscal and monetary policies.
The Equilibrium Nominal Rate of Interest
Irving Fischer argued that the nominal rate ought to increase one-for-one with expected inflation, E(i):
(5.4) r nom =r real + E(i)
When real interest rates are stable, changes in nominal rates ought to predict changes in inflation
rates.
Taxes and the Real Rate of Interest
Tax liabilities are based on nominal income and the tax rate determined by the investor’s tax bracket.
The real after-tax rate is approximately the after-tax nominal rate minus the inflation rate:
(5.5) r nom ( 1−t )−i=( r real +i )−i=r real ( 1−t )−it
Because you pay taxes on even the portion of interest earnings that is merely compensation for inflation, your
after-tax real returns falls by the tax rate times the inflation rate.
5.2 Comparing Rates of Return for Different Holding Periods
Zero-coupon bonds are sold at a discount form par value and provide their entire return from the difference
between the purchase price and the ultimate repayment of par value.
100
(5.6) r f ( T )= −1
P(T )
We typically express all investment returns as an effective annual rate (EAR), defined as the percentage
increase in funds invested over a 1-year horizon.
In general, we can relate EAR to the total return, r f(T), over a holding period of length T by using:
1 /T
(5.7) 1+ EAR=[ 1+r f ( T ) ]
Annual Percentage Rates
Annualized rates on short-term investments often are reported using simple rather than compound interest.
Annual percentage rates (APRs)
The relationship among the compounding period, the EAR, and the APR is:
n 1/ T
1+ EAR=[ 1+r f ( T ) ] =[ 1+ r f ( T ) ] = [ 1+T × APR ]
1/ T
(5.8)
Equivalently,
(1+ EAR )T −1
APR=
T
Continuous Compounding
As T approaches zero, we effectively approach continuous compounding (CC), and the relation of EAR to the
annual percentage rate, denoted by rcc for the continuously compounded case, is given by the exponential
function
2
,(5.9) 1+ EAR=exp ( r cc )=e r cc
To find rcc from the effective annual rate, we solve (5.9) for r cc as follows:
ln ( 1+ EAR )=r cc
ln() is the natural logarithm function, the inverse of exp().
The total return scales up in direct proportion to the time period, T.
5.3 Bills and Inflation, 1926-2015
We divide the sample period at 1952. After that year, inflation is far less volatile, and, probably as a result, the
nominal interest rate tracks the inflation rate with far greater precision, resulting in a far more stable real
interest rate.
Dramatic reduction in the standard deviation of the real rate.
The lower standard deviation of the real rate in the post-1952 period reflects a similar decline in the standard
deviation of the inflation rate.
Fischer’s relation appears to work far better when inflation is itself more predictable and investors can more
accurately gauge the nominal interest rate they require to provide an acceptable real rate of return.
5.4 Risk and Risk Premiums
Holding-Period Returns
With an investment horizon of 1 year, the realized rate of return on your investment will depend on:
a. The price per share at year’s end; and
b. The cash dividends you will collect over the year.
Holding period return
Ending price of a share−Beginning price +Cash dividend
(5.10) HPR=
Beginning price
The percent return from dividends is called the dividend yield, and so dividend yield plus the rate of capital
gains equals HPR.
Expected Return and Standard Deviation
(5.11) E ( r )= ∑ p ( s ) r ( s )
s
The variance of the rate of return (2) is a measure of volatility. It measures the dispersion of possible
outcomes around the expected value. Volatility is reflected in deviations of actual returns from the mean
return.
σ 2=∑ p ( s ) [ r ( s )−E ( r ) ]
2
(5.12)
s
To get back to original units, we calculate the standard deviations as the square root (√) of variance.
Excess Returns and Risk Premiums
We measure the reward as the difference between the expected HPR on the index stock fund and the risk-free
rate, that is, the rate you would earn in risk-free assets.
The difference: risk premium on common stocks
The difference in any particular period between the actual rate of return on a risky asset and the actual risk-
free rate is called the excess return.
3
, The risk premium is the expected value of the excess return
The standard deviation of the excess return is a measure of its risk
The degree to which investors are willing to commit funds to stocks depends on their risk aversion.
If the risk premium were zero, they would not invest any money in stocks.
General rule: the maturity of the risk-free rate should match the investment horizon.
5.5 Time Series Analysis of Past Rates of Return
Expected Returns and the Arithmetic Average
n n
1
(5.13) E ( r )=∑ p ( s ) r ( s )= ∑ r ( s )
s=1 n s=1
Arithmetic average of historic rates of return
The Geometric (Time-Weighted) Average Return
The arithmetic average provides an unbiased estimate of the expected future return.
An intuitive measure of performance over the sample period is the (fixed) annual HPR that would compound
over the period to the same terminal value obtained from the sequence of actual returns in the time series.
(5.14) ( 1+ g )n=Terminal value=( 1+ r 1 ) × ( 1+r 2 ) … ×(1+ r n)
g=Terminal valu e1 /n
Practitioners call g the time-weighted average return to emphasize that each past return receives an equal
weight in the process of averaging.
If returns come from a normal distribution, the expected difference is exactly half the variance of the
distribution, that is,
1
(5.15) E [ Geometric average ] =E [ Arithmetic average ] = σ 2
2
Variance and Standard Deviation
Because we cannot directly observe expectations, we calculate variance by averaging squared deviations from
our estimate of the expected return, the arithmetic average, ŕ .
Variance=Expected value of squared deviations
σ 2=∑ p ( s ) [ r ( s )−E ( r ) ]
2
Using historical data with n observations, we could estimate variance as
n
1 2
(5.16) σ^ 2= ∑ [ r ( s )−ŕ ]
n s=1
This estimate is biased downward. The reason is that we have taken deviations from the sample arithmetic
average instead of the unknown, true expected value, and so have introduced an estimation error.
A degrees of freedom bias
We can eliminate the bias by multiplying the arithmetic average of squared deviations by the factor n/(n – 1):
n n
(5.17) σ
2
( )
^ = n × 1 ∑ [ r ( s )− ŕ ] = 1 ∑ [ r ( s ) −ŕ ]
n−1 n s=1
2
1−n s=1
2
4
Voordelen van het kopen van samenvattingen bij Stuvia op een rij:
Verzekerd van kwaliteit door reviews
Stuvia-klanten hebben meer dan 700.000 samenvattingen beoordeeld. Zo weet je zeker dat je de beste documenten koopt!
Snel en makkelijk kopen
Je betaalt supersnel en eenmalig met iDeal, creditcard of Stuvia-tegoed voor de samenvatting. Zonder lidmaatschap.
Focus op de essentie
Samenvattingen worden geschreven voor en door anderen. Daarom zijn de samenvattingen altijd betrouwbaar en actueel. Zo kom je snel tot de kern!
Veelgestelde vragen
Wat krijg ik als ik dit document koop?
Je krijgt een PDF, die direct beschikbaar is na je aankoop. Het gekochte document is altijd, overal en oneindig toegankelijk via je profiel.
Tevredenheidsgarantie: hoe werkt dat?
Onze tevredenheidsgarantie zorgt ervoor dat je altijd een studiedocument vindt dat goed bij je past. Je vult een formulier in en onze klantenservice regelt de rest.
Van wie koop ik deze samenvatting?
Stuvia is een marktplaats, je koop dit document dus niet van ons, maar van verkoper bleussink. Stuvia faciliteert de betaling aan de verkoper.
Zit ik meteen vast aan een abonnement?
Nee, je koopt alleen deze samenvatting voor €3,49. Je zit daarna nergens aan vast.
Is Stuvia te vertrouwen?
4,6 sterren op Google & Trustpilot (+1000 reviews)
Afgelopen 30 dagen zijn er 52355 samenvattingen verkocht
Opgericht in 2010, al 14 jaar dé plek om samenvattingen te kopen