Samenvatting
Summary Overview of tests MRM1
- Instelling
- Universiteit Van Amsterdam (UvA)
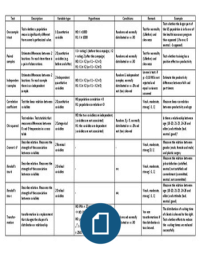
This document contains an overview of the formulas that are thought in MRM1. It gives a nice overview of all formulas, there meaning and helps to understand them.
[Meer zien]