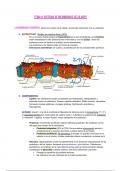
Hoofdstuk 5 Integratietechnieken
De kettingregel en de substitutieregel
Bij de functie u ( x )=f ( g ( x ) ) gebruiken we de kettingregel om de afgeleide te vinden, dit geeft
' '
u' ( x ) =f ( g ( x ) ) ∙ g ( x )
Om weer terug te komen bij u ( x ), ofwel de primitieve van u' ( x ) , nemen we het integraal van u' ( x )
' '
gebruik makende van de substitutieregel∫ f ( g ( x ) ) ∙ g ( x ) dx=f ( g ( x ) )
4
Als voorbeeld nemen we het integraal 4 x3 e x (voorwaarde is dat 4 x3 de afgeleideis van x 4 is )
u ( x )=x 4 u' ( x ) =¿ 4 x3
4 4
∫ 4 x 3 e x dx =∫ u' ( x ) ∙ e u ( x ) dx=∫ e u (x ) dx=¿ eu ( x ) +C=e x +C ¿
Voor willekeurige functies f ( u ) en u=u ( x ) geldt:
∫ f ( u ( x ) ) ∙ u' ( x ) dx=∫ f ( u ) du
Als een functie niet de vorm heeft die voor substitutie nodig is dan moet het integrand met een
constante factor worden vermenigvuldigt.
TIP!
Voorbeeld
Bepaal van u(x) de afgeleide en
g ( x )=cos ( 2 x ) probeer deze terug te vinden in het
u ( x )=2 x integrand, is deze niet terug te vinden,
g ( x )=cos ( u ( x ) ) vermenigvuldig dan het integrand met
u' ( x )=2
de factor die ervoor zorgt dat het
Integrand heeft niet de vorm “u' ( x ) ∙ cos ( u ( x ) )” integrand de vorm “u' ( x ) f (u ( x ) )”
krijgt.
Immers nu staat er g ( x )=1∙ cos ( u ( x ) ) dus moet er
Compenseer door het integraal te
vermenigvuldigt worden met een constante factor, vermenigvuldigen met
maar welke?
1
Constante factor = 2/1=2 en dit geeft: constante factor
2 ∙cos ( u ( x ) ) dit kan door middel van de
substitutieregel geprimitiveerd worden (rekening houdend met compensatiefactor:
1 1 1
∫ 2∙ cos ( u ( x ) )=¿ cos ( u ( x ) ) = cos ( 2 x ) +C ¿
2 2 2
De kettingregel en de substitutieregel
Bij de functie u ( x )=f ( g ( x ) ) gebruiken we de kettingregel om de afgeleide te vinden, dit geeft
' '
u' ( x ) =f ( g ( x ) ) ∙ g ( x )
Om weer terug te komen bij u ( x ), ofwel de primitieve van u' ( x ) , nemen we het integraal van u' ( x )
' '
gebruik makende van de substitutieregel∫ f ( g ( x ) ) ∙ g ( x ) dx=f ( g ( x ) )
4
Als voorbeeld nemen we het integraal 4 x3 e x (voorwaarde is dat 4 x3 de afgeleideis van x 4 is )
u ( x )=x 4 u' ( x ) =¿ 4 x3
4 4
∫ 4 x 3 e x dx =∫ u' ( x ) ∙ e u ( x ) dx=∫ e u (x ) dx=¿ eu ( x ) +C=e x +C ¿
Voor willekeurige functies f ( u ) en u=u ( x ) geldt:
∫ f ( u ( x ) ) ∙ u' ( x ) dx=∫ f ( u ) du
Als een functie niet de vorm heeft die voor substitutie nodig is dan moet het integrand met een
constante factor worden vermenigvuldigt.
TIP!
Voorbeeld
Bepaal van u(x) de afgeleide en
g ( x )=cos ( 2 x ) probeer deze terug te vinden in het
u ( x )=2 x integrand, is deze niet terug te vinden,
g ( x )=cos ( u ( x ) ) vermenigvuldig dan het integrand met
u' ( x )=2
de factor die ervoor zorgt dat het
Integrand heeft niet de vorm “u' ( x ) ∙ cos ( u ( x ) )” integrand de vorm “u' ( x ) f (u ( x ) )”
krijgt.
Immers nu staat er g ( x )=1∙ cos ( u ( x ) ) dus moet er
Compenseer door het integraal te
vermenigvuldigt worden met een constante factor, vermenigvuldigen met
maar welke?
1
Constante factor = 2/1=2 en dit geeft: constante factor
2 ∙cos ( u ( x ) ) dit kan door middel van de
substitutieregel geprimitiveerd worden (rekening houdend met compensatiefactor:
1 1 1
∫ 2∙ cos ( u ( x ) )=¿ cos ( u ( x ) ) = cos ( 2 x ) +C ¿
2 2 2